개요

Tree 문제 모음

pre-order 구현 - Tree: Preorder Traversal
post-order 구현 - Tree: Postorder Traversal
in-order 구현 - Tree: Inorder Traversal
tree의 높이 구하기 - Tree: Height of a Binary Tree

이번에는 Tree 자료구조에 대한 문제를 풀어보았다.

tree의 특징

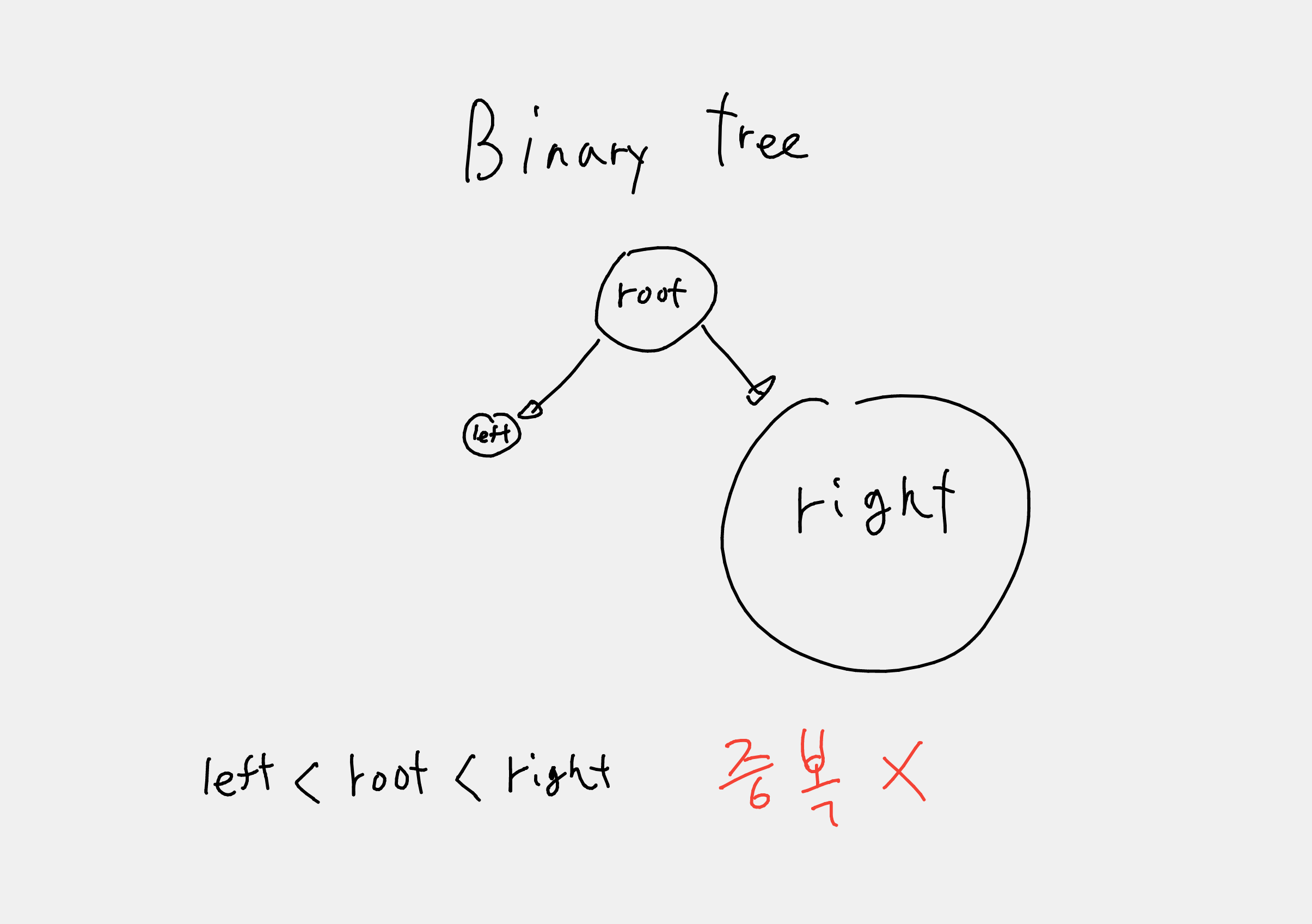
Tree란 아래의 그림처럼 binary tree가 유명하며, 아래와 같이 root 밑에 left, right가지로 구성되어 있는 형태이다.

데이터를 중복 없이 저장하고, 데이터 검색 시 O(logN)¹ 이라는 빠른 장점이 있다. 단, 아래의 그림처럼 left < root < right를 만족할 때 자료구조의 검색이 용이해진다.

tree의 탐색 방법

tree를 탐색하는 여러가지 방법이 있는데, 1~3 번 문제가 바로 그 종류이다.

탐색하는 방법은 pre, post, in 이 있으며 아래의 그림과 같은 순서를 만족한다.

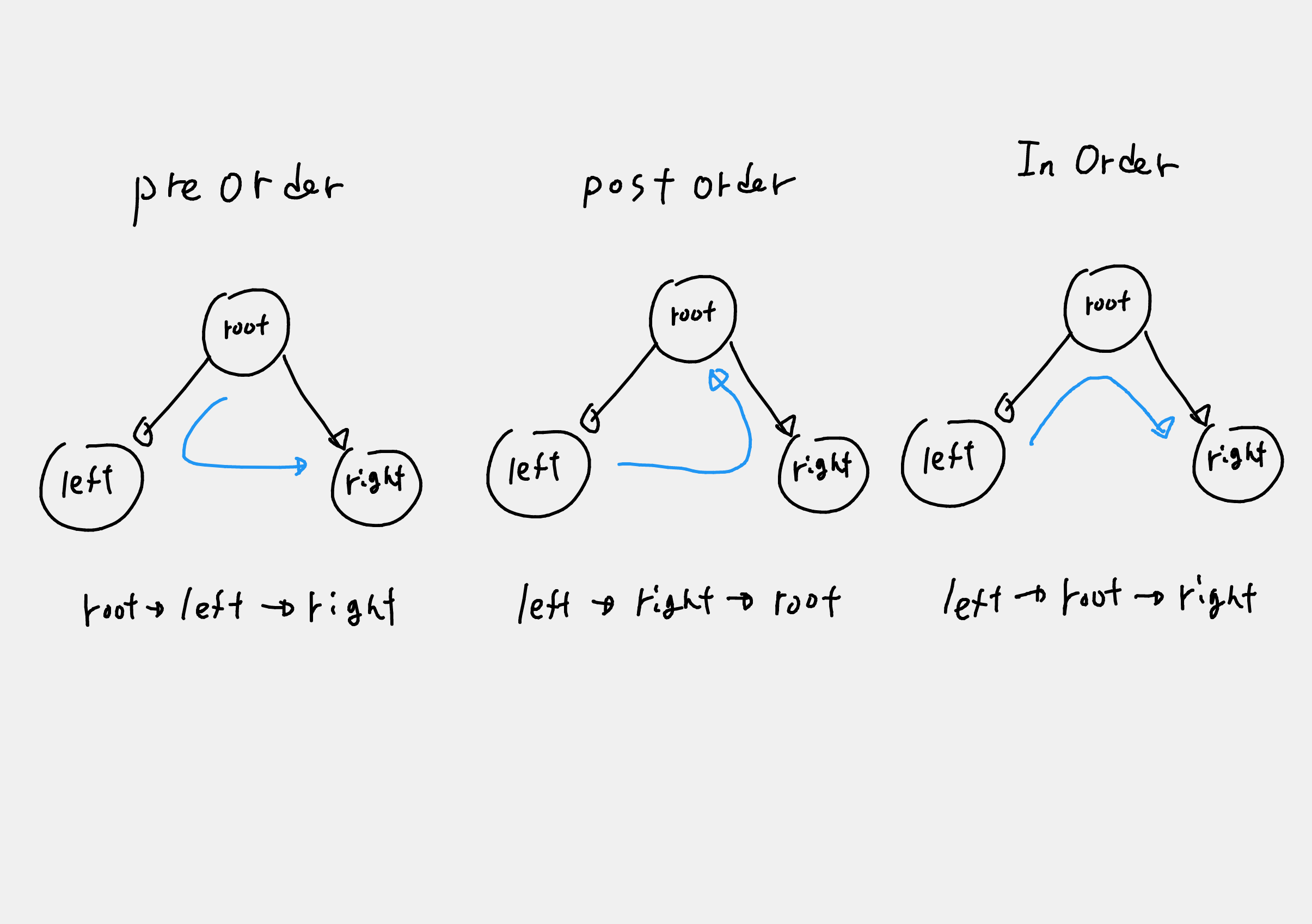
각각의 탐색방법을 구현할 때는 다음에 소개할 재귀 함수 형태로 구현하는 것이 쉽다.

pre-order 탐색 방법 구현

pre-order를 구현한 코드이다. root -> left -> right 순서대로 호출 한다.

pre-order.py
def preOrder(root):
    # root -> left -> right
    print(root.info,end=" ")
    if root.left is not None:
        preOrder(root.left)
    if root.right is not None:
        preOrder(root.right)

post-order 탐색 방법 구현

post-order를 구현한 코드이다. left -> right -> root 순서대로 호출 한다.

post-order.py
def postOrder(root):
    # left -> right -> root
    if root.left is not None:
        postOrder(root.left)
    if root.right is not None:
        postOrder(root.right)
    print(root.info,end=" ")

in-order 탐색 방법 구현

in-order를 구현한 코드이다. left -> root -> right 순서대로 호출 한다.

in-order.py
def inOrder(root):
    # left -> root -> right
    if root.left is not None:
        inOrder(root.left)
    print(root.info,end=" ")
    if root.right is not None:
        inOrder(root.right)

tree의 높이 구하기

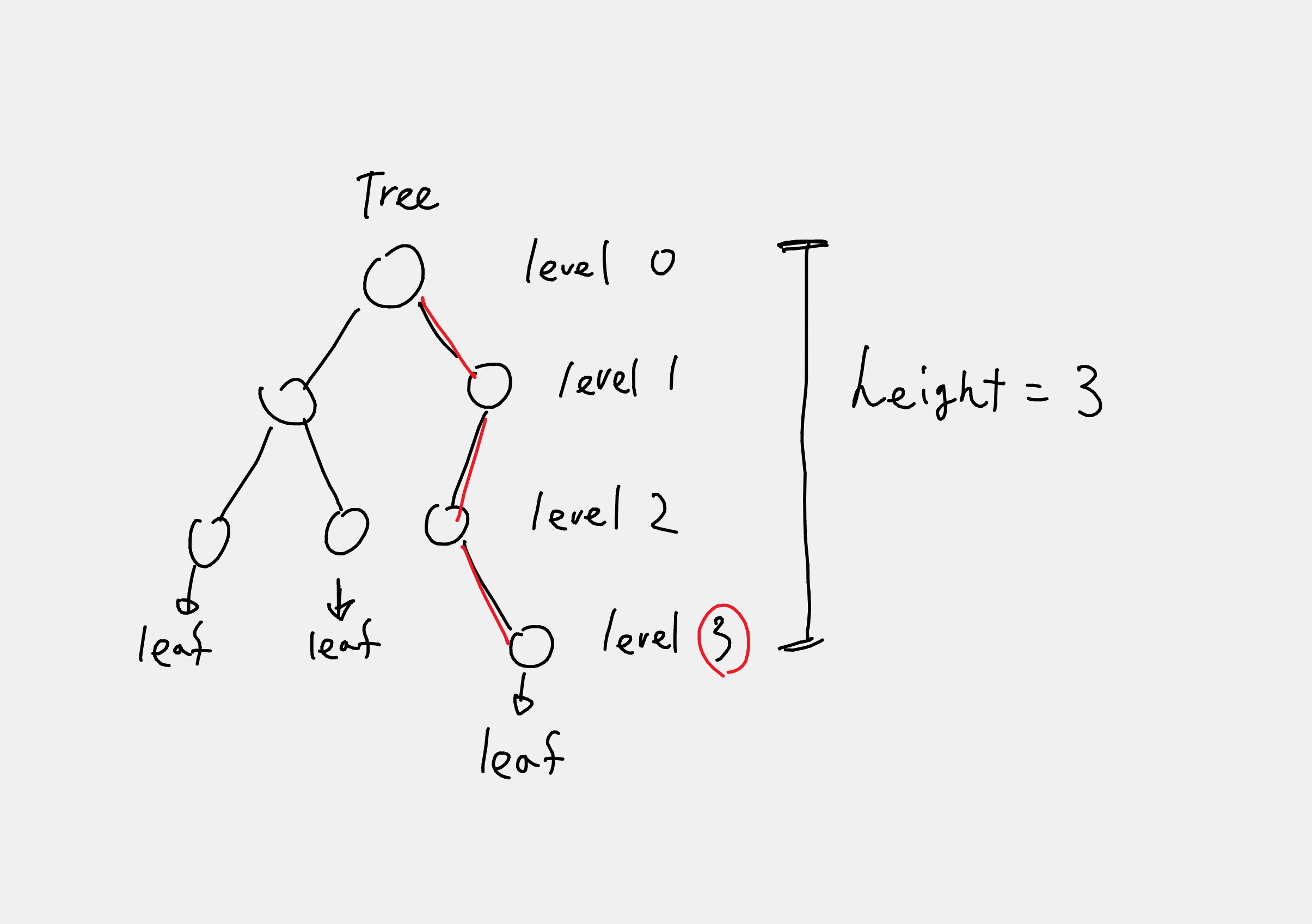
tree의 높이를 구하려고한다. 아래의 그림처럼 tree의 잎사귀 Node² 노드의 최대 level이 tree의 높이라고 말한다.

탐색 할 case 작성

tree를 높이를 구할 아래의 case를 나누어서 생각해야 할 것이다.

높이 구하기 case

1. left 및 right가 전부 있을 때
2. left 만 있을 때
3. right 만 있을 때
4. left 및 right가 전부 없을 때

4번 같은 경우 잎사귀 Node가 없으므로 높이는 0이다. 2번,3번 같은 경우 각각 존재하므로 높이는 적어도 1이 추가되어야 한다.

문제는 1번인데 left 또는 right가 어디까지 뻗어있는지 모르는 상황이므로 적어도 높이는 1개이고, 두 Node의 최대 값을 구하면 된다.

이를 구현한 코드는 아래와 같다.

get-height.py
def height(root):
    if  root.left and root.right: # 1번 case
        return 1 + max(height(root.left),height(root.right))
    elif root.left and root.right is None: # 2번 case
        return 1 + height(root.left)
    elif root.left is None and root.right: # 3번 case
        return 1 + height(root.right)
    else: # 4번 case
        return 0

#hackerrank #problem solving #data structures #Tree

한번 검색 시, 탐색해야 할 데이터의 개수가 1/2로 줄어들기 때문이다. ↩
잎사귀 Node란 left 및 right가 없는 제일 끝의 Node를 의미한다. ↩

개요